A BETTER METHOD TO RECALCULATE NORMALS IN UNITY

原文链接

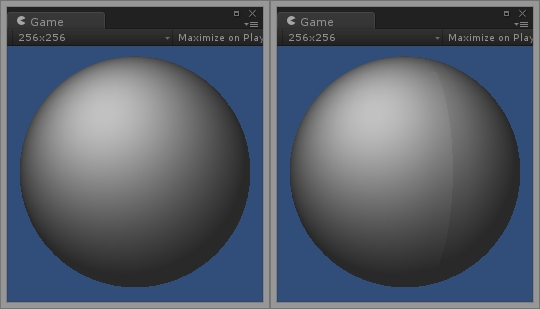
A visible seam showing after recalculating normals in runtime.

You might have noticed that, for some meshes, calling Unity’s built-in function to RecalculateNormals(), things look different (i.e. worse) than when calculating them from the import settings. A similar problem appears when recalculating normals after combining meshes, with obvious seams between them. For this post I’m going to show you how RecalculateNormals() in Unity works and how and why it is very different from Normal calculation on importing a model. Moreover, I will offer you a fast solution that fixes this problem.

This article is also very useful to those who want to generate 3D meshes dynamically during gameplay and not just those who encountered this problem.

Some background…

I’m going to explain some basic concepts as briefly as I can, just to provide some context. Feel free to skip this section if you wish.

Directional Vectors

Directional vectors are not to be confused with point vectors, even though we use exactly the same representation in code. Vector3(0, 1, 1) as a point vector simply describes a single point along the X, Y and Z axis respectively. As a directional vector, it describes the direction we have when we stand at the origin point (Vector3(0, 0, 0) ) and look towards the point Vector3(0, 1, 1) .

If we draw a line from Vector3(0, 0, 0) towards Vector3(0, 1, 1) , we will notice that this line has a length of 1.414214 units. This is called the magnitude or length of a vector and it is equal to sqrt(X^2 + Y^2 + Z^2). A normalized vector is one that has a magnitude of 1. The normalized version of Vector3(0, 1, 1 ) is Vector3(0, 0.7, 0.7) and we get that by dividing the vector by its magnitude. When using directional vectors, it is important to keep them normalized (unless you really know what you’re doing), because a lot of mathematical calculations depend on that.

Normals

Normals are mostly used to calculate the shading of a surface. They are directional vectors that define where a surface is “looking at”, i.e. it is a directional vector that is pointing away from a face (i.e. a surface) made up of three or more vertices (i.e. points). More accurately, normals are actually stored on the vertices themselves instead of the face. This means that a flat surface of three points actually has three identical normals.

A normal is not to be confused with a normalized vector, although normals are normalized – otherwise, light calculations would look wrong.

How Smoothing works

Smoothing works by averaging the normals of adjacent faces. What this means is that the normal of each vertex is not the same as that of its face, but rather the average value of the normals of all the faces it belongs to. This also means that, in smooth shading, vertices of the same face do not necessarily have identical normals.

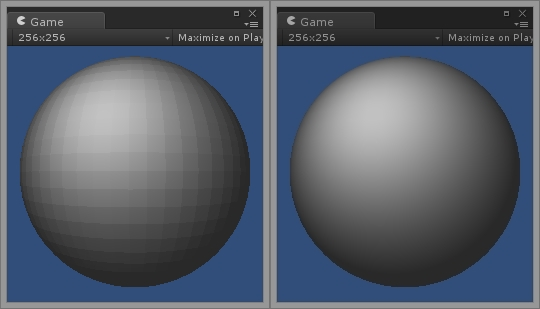
A sphere with flat and smooth shading.

How Unity recalculates normals in runtime

When you call the RecalculateNormals() method on a mesh in Unity, what happens is very straightforward.

Unity stores mesh information for a list of vertices in a few different arrays. There’s one array for vertex positions, one array for normals, another for UVs, etc. All of these arrays have the same size, and each information of one index in the array represent one single vertex. For example, mesh.vertices[N] and mesh.normals[N] are the position and the normal, respectively, of the Nth vertex in our list of vertices.

However, there is a special array called triangles and it describes the actual faces of the mesh. It is a sequence of integer values, and each integer is the index of a vertex. Each three integers form a single triangle face. This means that the size of this array is always a multiple of 3.

As a side note: Unity assumes that all faces are triangles, so even if you import a model with faces having more than three points (as is the case with the sphere above), they’re automatically converted, upon importing, to multiple smaller faces of three vertices each.

The source code of RecalculateNormals() is not available, but, guessing from its output, this pseudo-code (sloppily mixed with some real code) follows exactly the same algorithm and produces the same result:

initialize all normals to (0, 0, 0)

foreach three indices in triangles list of mesh:
	normal = CalculateSurfaceNormal(
		mesh.vertices[index1],
		mesh.vertices[index2],
		mesh.vertices[index3])
	mesh.normals[index1] += normal
	mesh.normals[index2] += normal
	mesh.normals[index3] += normal

foreach vertex in mesh:
	normalize vertex.normal
}

Notice how I don’t explicitly average the normals, but that’s because CalculateSurfaceNormal(…) is assumed to return a normalized vector. When normalizing a sum of normalized vectors, we get their average value.

How Unity calculates normals while importing

The exact algorithm Unity uses in this case is more complicated than RecalculateNormals() . I can think of three reasons for that:

1. This algorithm is much slower to use, so Unity avoids calling that during runtime.
2. Unity has more information while importing.
3. Unity combines vertices after importing.

The first reason is not the real reason because Unity could have still provided an alternative method to calculate normals in runtime that still performs fast enough. The second and third reasons are actually very similar, since they both come down to one thing: After Unity imports a mesh, it becomes a new entity independent from its source model.

During mesh import, Unity may consider shared vertices among faces to exist multiple times; one time for each face.This means that when importing a cube, which has 8 vertices, Unity actually sees 36 vertices (3 vertices for each of the 2 triangles of each one of the 6 sides). We will refer to this as the expanded vertex list. However, it can also see the condensed 8 vertex list at the same time. If it can’t, then I’m guessing it first silently builds that structure simply by finding which vertices are at the same position as other vertices.

As you saw in the previous section, smoothing in RecalculateNormals() only works when vertices at the same position are assumed to be one and the same. With this new data at hand, a different algorithm is to be used. In the following pseudo-code, vertex represents a vertex from the condensed list of vertices and vertexPoint represents a vertex from the expanded list. We also assume that any vertexPoint has direct access to the vertex it is associated to.

threshold = ?

initialize all vertexPoint normals to (0, 0, 0)

foreach vertexPoint in mesh:
	foreach testFace in vertexPoint.vertex.faceList:
		if angle between vertexPoint.face.normal and testFace.normal < threshold
			vertexPoint.normal += testFace.normal

foreach vertexPoint in mesh:
	normalize vertexPoint.normal

As it turns out, the final result contains neither the expanded vertex list nor the condensed vertex list. It is an optimized version which takes all the identical vertices and merges them together. And by identical, I don’t mean just the position and normals; it also also takes into account all the UV coordinates, tangents, bone weights, colors, etc – any information that is stored for a single vertex.

The problem explained

As you may have guessed from the previous section, the problem is that vertices that differ in one or more aspects are considered as completely different vertices in the final mesh that is used during runtime, even if they share the same position. You will most likely encounter this problem when your model has UV coordinates. In fact, the first image of this article was produced precisely by a model with a UV seam, after RecalculateNormals() was called.

I will not get into many details about UV coordinates, but let me just say that they’re used for texturing, which means it is actually a very common problem; if you ever recalculate normals at runtime then this situation is bound to appear sooner or later.

You can also see this problem if you’re merging two meshes together – say, two opposing halves of a sphere – even if they have identical information. That’s because when merging two meshes, what actually happens is that we simply append the data of one mesh on top of another, which leads common vertices between the two to be distinct in the final mesh.

The technical cause behind the problem is, as we have pointed out, that RecalculateNormals() does not know which distinct vertices in our list have the same position as others. Unity knows this while importing, but this information is now lost.

This is also the reason RecalculateNormals() does not take any angle threshold as a parameter, contrary to calculating normals during import time. If I import a model with a 0° tolerance, then it will be impossible to have any smooth shading during run-time.

My solution

My solution to this problem is not very simple, but I have provided the full source code. It is somewhat of a hybrid solution between the two extremes used by Unity. I use hashing to cluster vertices that exist in the same position to achieve a nearly linear complexity (based on the number of vertices in the expanded list) to avoid a brute-force approach. Therefore, it is fast and asymptotically optimal. However, it does allocate a bunch of temporary memory which might cause a bit of a lag.

Usage

By adding my code to your project (found at the end of this article), you will be able to recalculate normals based on an angle threshold:

var mesh = GetComponentInChildren().mesh;
mesh.RecalculateNormals(60);

As you probably know, comparing equality between two floating numbers is a bad practice, because of the inherent imprecision of this data type. The usual approach is to check whether the floats have a very small difference between them (say, 0.0001), but this is not enough in this case since I need to produce a hash key as well. I use a different approach that I loosely call “digit tolerance”, which compares floats by converting them to long integers after multiplying them with a power of 10. This method makes it very easy for Vector3 values to have identical hash codes if they’re identical within a given tolerance.

My implementation multiplies with the constant 100,000 (for 5 decimal digits), which means that 4.000002 is equal to 4.00000. The tolerance is rounded, so 4.000008 is equal to 4.00001. If we use a number that is either too small or too large then we will probably get wrong results. 100,000 is a good number, you will rarely need to change that. Feel free to do so if you think it’s better.

Things to be aware of

One thing to keep in mind is that my solution might smoothen normals even with an angle higher than the threshold; this only happens when we try to smoothen with an angle less than the one specified by the import settings. Don’t worry though, it is still possible to get the right result.

I could have written an alternative method that splits those vertices at runtime, or one that recreates a flat mesh and then merges identical vertices after smoothing. However, I thought that this was much bigger trouble than what it was worth and it would kill performance.

To achieve a better result, you can import a mesh with a 0° tolerance. This will allow you to smooth normals at any angle during runtime. However, since a 0° tolerance produces a larger model, you can also just import a mesh with the minimum tolerance you’re ever going to need. If you import at 30°, you can still smooth correctly at runtime for any degree that is higher than 30°.

In any case, a 60° tolerance is good for most applications. You can use that for both import and runtime normal calculation.

Edit 25/03/2017:

The code has been updated, so the old code has been omitted from this post. You can find the new code here!

Happy smoothing!

---

A BETTER METHOD TO RECALCULATE NORMALS IN UNITY – PART 2

It’s been over 2 years since I posted about a method to recalculate normals in Unity that fixes on some of the issues of Unity’s default RecalculateNormals() method. I’ve used this algorithm (and similar variations) myself in non-Unity projects and I’ve since made minor adjustments, but I never bothered to update the Unity version of the code. Someone recently reported to me that it fails when working with meshes with multiple materials, so I decided to go ahead and update it.

The most important performance update is that I now use FNV hashing to encode the vertex positions. The first implementation used a very naive hashing which would have many hashing collisions. A mesh with approximately a million vertices would end up with a significant amount of collisions, which was a performance killer.

Using FNV hashing reduced collisions to a negligible amount, even to 0 in most cases. I don’t have the figures now, as this change happened about a year ago, but I might do some newer measurements later (read: probably never).

To summarize, here are the changes:

• Fixed issue with multiple materials not working properly.
• Changed VertexKey to use FNV hashing.
• Other (minor) performance improvements.

And I know you’re here just for the code, so here it is:

/* 
 * The following code was taken from: http://schemingdeveloper.com
 *
 * Visit our game studio website: http://stopthegnomes.com
 *
 * License: You may use this code however you see fit, as long as you include this notice
 *          without any modifications.
 *
 *          You may not publish a paid asset on Unity store if its main function is based on
 *          the following code, but you may publish a paid asset that uses this code.
 *
 *          If you intend to use this in a Unity store asset or a commercial project, it would
 *          be appreciated, but not required, if you let me know with a link to the asset. If I
 *          don't get back to you just go ahead and use it anyway!
 */

using System;
using System.Collections.Generic;
using UnityEngine;

public static class NormalSolver
{
    /// <summary>
    ///     Recalculate the normals of a mesh based on an angle threshold. This takes
    ///     into account distinct vertices that have the same position.
    /// </summary>
    /// <param name="mesh"></param>
    /// <param name="angle">
    ///     The smoothing angle. Note that triangles that already share
    ///     the same vertex will be smooth regardless of the angle! 
    /// </param>
    public static void RecalculateNormals(this Mesh mesh, float angle) {
        var cosineThreshold = Mathf.Cos(angle * Mathf.Deg2Rad);

        var vertices = mesh.vertices;
        var normals = new Vector3[vertices.Length];

        // Holds the normal of each triangle in each sub mesh.
        var triNormals = new Vector3[mesh.subMeshCount][];

        var dictionary = new Dictionary<VertexKey, List<VertexEntry>>(vertices.Length);

        for (var subMeshIndex = 0; subMeshIndex < mesh.subMeshCount; ++subMeshIndex) {
            
            var triangles = mesh.GetTriangles(subMeshIndex);

            triNormals[subMeshIndex] = new Vector3[triangles.Length / 3];

            for (var i = 0; i < triangles.Length; i += 3) {
                int i1 = triangles[i];
                int i2 = triangles[i + 1];
                int i3 = triangles[i + 2];

                // Calculate the normal of the triangle
                Vector3 p1 = vertices[i2] - vertices[i1];
                Vector3 p2 = vertices[i3] - vertices[i1];
                // By not normalizing the cross product,
                // the face area is pre-multiplied onto the normal for free.
                // Vector3 areaWeightedNormal = Vector3.Cross (p1, p2);
                Vector3 normal = Vector3.Cross(p1, p2).normalized;
                int triIndex = i / 3;
                triNormals[subMeshIndex][triIndex] = normal;

                List<VertexEntry> entry;
                VertexKey key;

                if (!dictionary.TryGetValue(key = new VertexKey(vertices[i1]), out entry)) {
                    entry = new List<VertexEntry>(4);
                    dictionary.Add(key, entry);
                }
                entry.Add(new VertexEntry(subMeshIndex, triIndex, i1));

                if (!dictionary.TryGetValue(key = new VertexKey(vertices[i2]), out entry)) {
                    entry = new List<VertexEntry>();
                    dictionary.Add(key, entry);
                }
                entry.Add(new VertexEntry(subMeshIndex, triIndex, i2));

                if (!dictionary.TryGetValue(key = new VertexKey(vertices[i3]), out entry)) {
                    entry = new List<VertexEntry>();
                    dictionary.Add(key, entry);
                }
                entry.Add(new VertexEntry(subMeshIndex, triIndex, i3));
            }
        }

        // Each entry in the dictionary represents a unique vertex position.

        foreach (var vertList in dictionary.Values) {
            for (var i = 0; i < vertList.Count; ++i) {

                var sum = new Vector3();
                var lhsEntry = vertList[i];

                for (var j = 0; j < vertList.Count; ++j) {
                    var rhsEntry = vertList[j];

                    if (lhsEntry.VertexIndex == rhsEntry.VertexIndex) {
                        sum += triNormals[rhsEntry.MeshIndex][rhsEntry.TriangleIndex];
                    } else {
                        // The dot product is the cosine of the angle between the two triangles.
                        // A larger cosine means a smaller angle.
                        var dot = Vector3.Dot(
                            triNormals[lhsEntry.MeshIndex][lhsEntry.TriangleIndex],
                            triNormals[rhsEntry.MeshIndex][rhsEntry.TriangleIndex]);
                        if (dot >= cosineThreshold) {
                            sum += triNormals[rhsEntry.MeshIndex][rhsEntry.TriangleIndex];
                        }
                    }
                }

                normals[lhsEntry.VertexIndex] = sum.normalized;
            }
        }

        mesh.normals = normals;
    }

    private struct VertexKey
    {
        private readonly long _x;
        private readonly long _y;
        private readonly long _z;

        // Change this if you require a different precision.
        private const int Tolerance = 100000;

        // Magic FNV values. Do not change these.
        private const long FNV32Init = 0x811c9dc5;
        private const long FNV32Prime = 0x01000193;

        public VertexKey(Vector3 position) {
            _x = (long)(Mathf.Round(position.x * Tolerance));
            _y = (long)(Mathf.Round(position.y * Tolerance));
            _z = (long)(Mathf.Round(position.z * Tolerance));
        }

        public override bool Equals(object obj) {
            var key = (VertexKey)obj;
            return _x == key._x && _y == key._y && _z == key._z;
        }

        public override int GetHashCode() {
            long rv = FNV32Init;
            rv ^= _x;
            rv *= FNV32Prime;
            rv ^= _y;
            rv *= FNV32Prime;
            rv ^= _z;
            rv *= FNV32Prime;

            return rv.GetHashCode();
        }
    }

    private struct VertexEntry {
        public int MeshIndex;
        public int TriangleIndex;
        public int VertexIndex;

        public VertexEntry(int meshIndex, int triIndex, int vertIndex) {
            MeshIndex = meshIndex;
            TriangleIndex = triIndex;
            VertexIndex = vertIndex;
        }
    }
}

After you include this code in your project, all you have to do is call RecalculateNormals(angle) on your mesh. Make sure you visit the original post for additional information about the algorithm.

A final note

This is not the most optimal way of doing this. It’s meant for one-off calculation only. If you do this over and over again you’d better use some sort of acceleration structure where you can query nearby vertices quickly (if the faces are expected to change) or build some kind of structure which contains all the proper neighbours per vertex.