AC自动机：如何实现敏感词过滤?

发表于 | 分类于

AC自动机：如何实现敏感词过滤

原文链接

文章目录

  • 敏感词过滤
  • AC自动机
  • 失效指针
  • 匹配
  • 完整代码
  • 性能计算

敏感词过滤

在一些社交平台如微博、微信、网络游戏等地方，难免会有一些不法分子散播色情、反动等内容，亦或是网友们的互相谩骂、骚扰等。为了净化网络环境，各大社交平台中都会有敏感词过滤的机制，将那些不好的词汇屏蔽或者替换掉

那你是否有想过，这个功能是如何实现的呢？

在我之前的博客中，介绍了四种单模式字符串匹配算法，分别是BF、RK、BM、KMP，以及一种多模式字符串匹配算法，Trie树。

对于单模式字符串匹配算法来说，如果我们要进行匹配，就需要针对每一个查询词来对我们输入的主串进行匹配，而随着词库的增大，匹配的次数也会变得越来越大，很显然，这种做法是行不通的。

那么我们再看看多模式字符串匹配算法，Trie树。对于Trie树来说，我们可以一次性将所有的敏感词都加入其中，然后再遍历主串，在树中查找匹配的字符串，如果找不到，则使Trie树重新回到根节点，再从主串的下一个位置开始找起。

Trie树的这种方法，就有点像BF中的暴力匹配，因为它没有一个合理的减少比较的机制，每当我们不匹配就需要从头开始查，大大的降低了执行的效率，对于一个高流量的社交平台来说这是不能容许的，毕竟没有人希望自己输入了一句话后要隔上一大段时间才能发出去。那么我们是否可以效仿KMP算法，添加一个类似next数组的机制来减少不必要的匹配呢？这也就是AC自动机的由来

AC自动机

AC自动机全程是Aho-CorasickAutoMaton，和Trie树一样是多模式字符串匹配算法。并且它与Trie树的关系就相当于KMP与BF算法的关系一样，AC自动机的效率要远远超出Trie树

AC自动机对Trie进行了改进，在Trie的基础上结合了KMP算法的思想，在树中加入了类似next数组的失效指针。

1
2
3
4
5
6
7
8
struct ACNode
{
    char _data;		//当前字符
    bool _isEnd;	//标记当前是否能构成一个单词
    int _length;    //当前模式串长度
    ACNode* _fail;  //失败指针
    unordered_map<char, ACNode*> _subNode;	//子节点
};

AC自动机的构建主要包含以下两个操作

  1. 将多个模式串构建成Trie树
  2. 为Trie树中每个节点构建失败指针

上述两个步骤看起来简单，但是理解起来十分复杂，如果不了解KMP算法和Trie树的话很难搞懂，所以如果对这两方面知识不熟的可以看看我往期的博客
在本篇博客中不会再次介绍KMP和Trie，如果需要了解的可以看看我的往期博客
Trie(字典树) : 如何实现搜索引擎的关键词提示功能？
字符串匹配算法(三)：KMP(KnuthMorrisPratt)算法

失效指针

例如我们具有这么一棵树

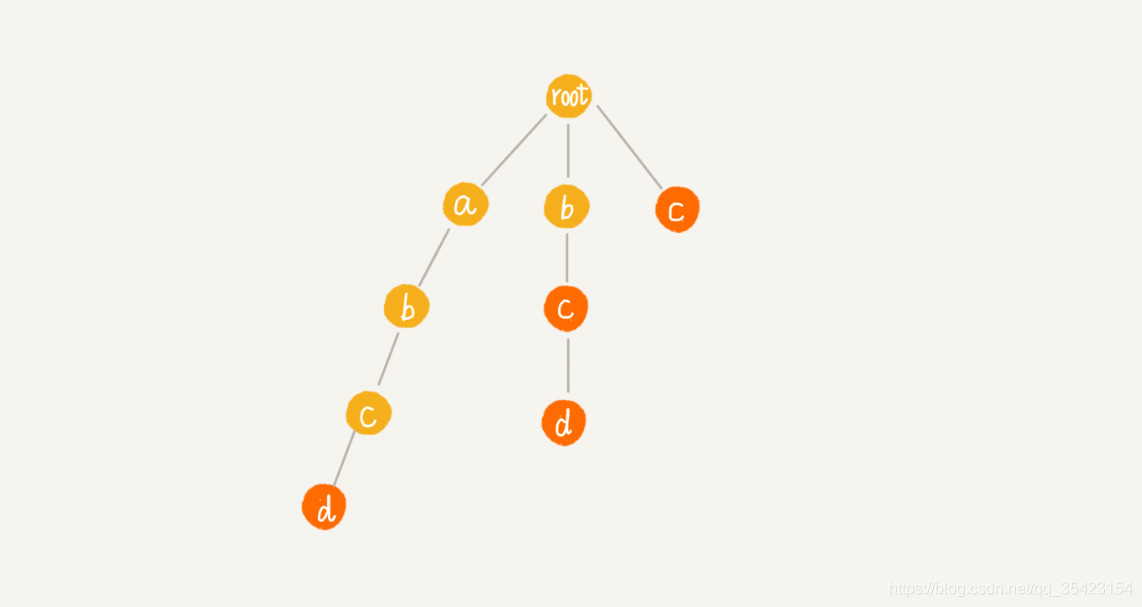
ac_am_1

如果要尽量减少匹配，我们就可以借助之前KMP的思想，通过找到可匹配的后缀子串或者前缀子串，将其对其，就可以减少中间多余的比对。

又由于Trie树是通过字符来划分子树，所以基于前缀的匹配不太容易理想(同一前缀的在同一条路径下，滑动效率不高)，那么我们就可以选择通过后缀来进行比对。

所以我们失败节点即为我们对其的位置，它的值与本节点值相同，并且失败指针指向的节点所构成的单词就是我们的后缀

首先，由于根节点不存数据，并且其没有父节点，所以它的失败指针为空。而我们又是基于字符划分的，所以在同一层中不可能有相同的节点，相同节点只能出现在相邻层中，并且我们又需要保证具有相同的后缀，所以得出结论，某个节点的失败指针只可能存在它的上层中。

基于以上两个特点，我们就可以直接推导出第一层节点的失败指针都为root。接着继续思考，如何构建下面的失败节点。

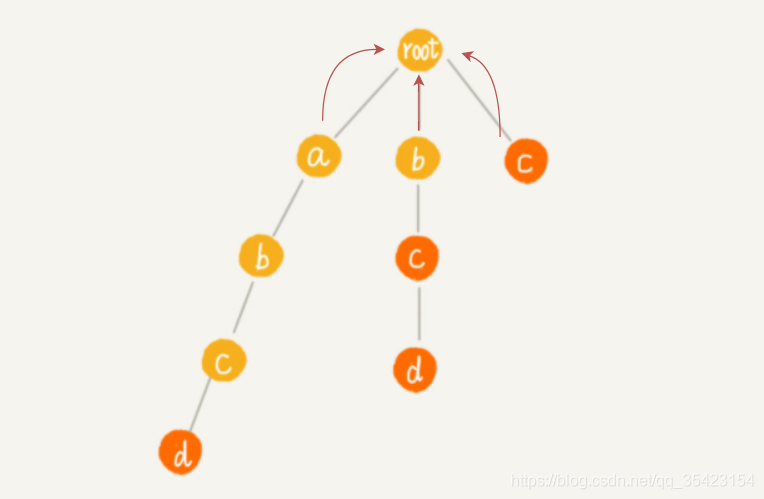
ac_am_2

那么如何求出子节点的失败指针呢？为保证失败指针指向的位置往上即为匹配的后缀，所以要使得后缀匹配，我们就需要到我们的失败指针中寻找与子节点匹配的节点，如果找不到，则沿着失败指针继续往它的失败指针继续寻找，如果到了最顶上还没有找到，则认为根节点为它的失败指针。

总结一下

  • 根节点的失败指针为空
  • 一个节点的失败指针只能在它的上层
  • 需要在父节点的失败节点中找到与子节点匹配的节点，如果找不到则沿着失败节点继续向上，找它的失败节点是否存在匹配节点，如果存在，则该节点就是子节点的失败节点。
  • 如果没有上层没有任何可匹配的节点，则失败指针指向根节点

为了方便理解过程，我一层一层往下进行构建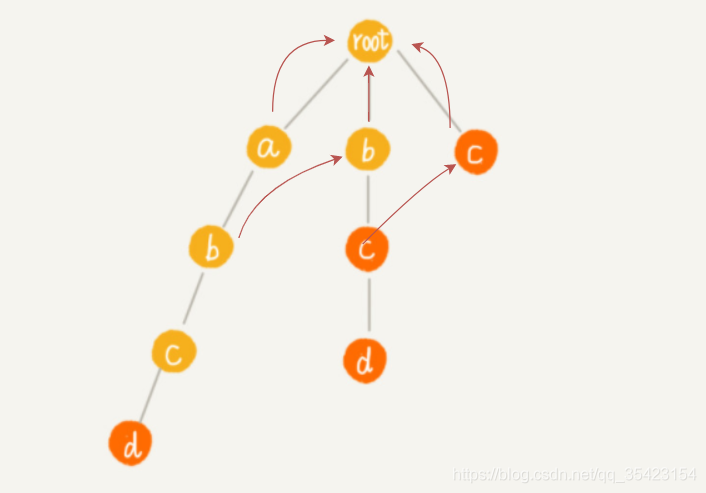
ac_am_3
由于前往a的失败节点root，可以找到匹配b的节点，所以将第二层的b作为子节点b的失败指针，c同理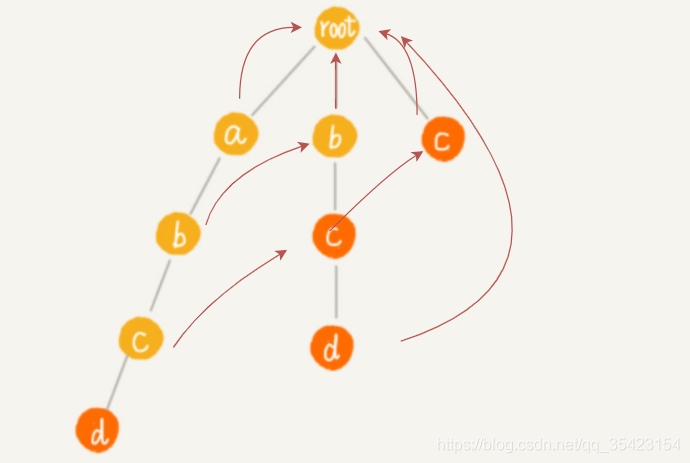
ac_am_4
c与上层同理，这里看d。由于d的父节点c的失败指针c中并不存在匹配节点，所以向c的失败指针继续寻找，由于c的失败指针为根节点，且也不存在匹配节点，此时已经到头，所以d的失败指针为根节点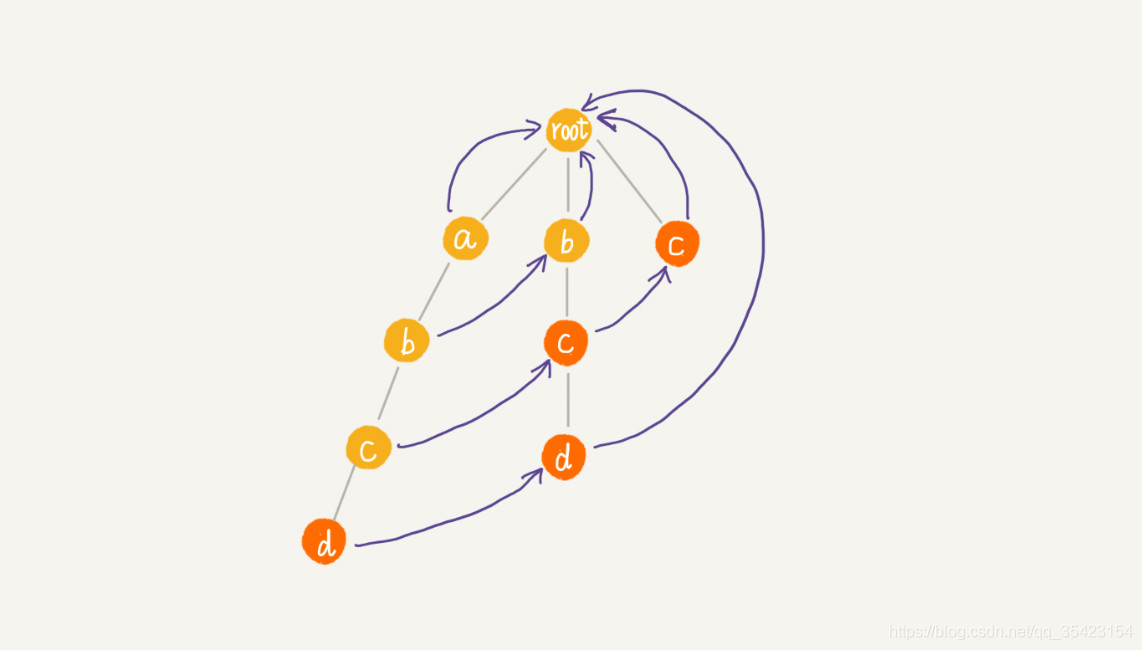
ac_am_5
最终构建结果

代码如下，详细思路都写在注释中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//构建失败指针
void AC::buildFailurePointer()
{
    //借助队列来完成层序遍历
    queue<ACNode*> q;
    q.push(_root);
    while (!q.empty())
    {
        ACNode* parent = q.front();
        q.pop();
        //遍历所有孩子节点
        for (auto& sub : parent->_subNode)
        {
            //如果父节点节点为根节点，则将孩子节点的失效指针全部设置为根节点
            if (parent == _root)
            {
                sub.second->_fail = _root;
            }
            else
            {
                ACNode* failParent = parent->_fail;    //父节点的失败指针
                while (failParent != nullptr)
                {
                    auto failChild = failParent->_subNode.find(sub.second->_data);    //寻找失败指针中是否存在一个子节点能与我们的子节点匹配
                    if (failChild != failParent->_subNode.end())   //如果存在，则这个子节点就是我们子节点的失败指针
                    {
                        sub.second->_fail = failChild->second;
                        break;
                    }
                    //如果找不到，则继续向上，寻找失败指针的失败指针是否有这么一个节点
                    failParent = failParent->_fail;
                }
                //如果一直找到最顶上也找不到，则将失败指针设置为根节点
                if (failParent == nullptr)
                {
                    sub.second->_fail = _root;
                }
            }
            //将子节点加入队列中
            q.push(sub.second);
        }
    }
}

匹配

讲了那么多原理，接下来就直接看看AC自动机是如何完成匹配的，此时主串为abcd，模式串为abcd，bc，bcd，c。

匹配主要包含以下两种规则

  1. 匹配成功时，如果当前并不是一个完整的模式串，则继续往下进行匹配。如果是一个完整的模式串，此节点匹配完成。但是匹配完成并不意味着中断，此时我们还要利用失败指针继续去匹配下一个查询词，所以直到我们的结果指针回到根节点之前，都会一直通过失败指针查找匹配的模式串
  2. 如果匹配失败，则前往失败指针中继续匹配，不断重复这一过程

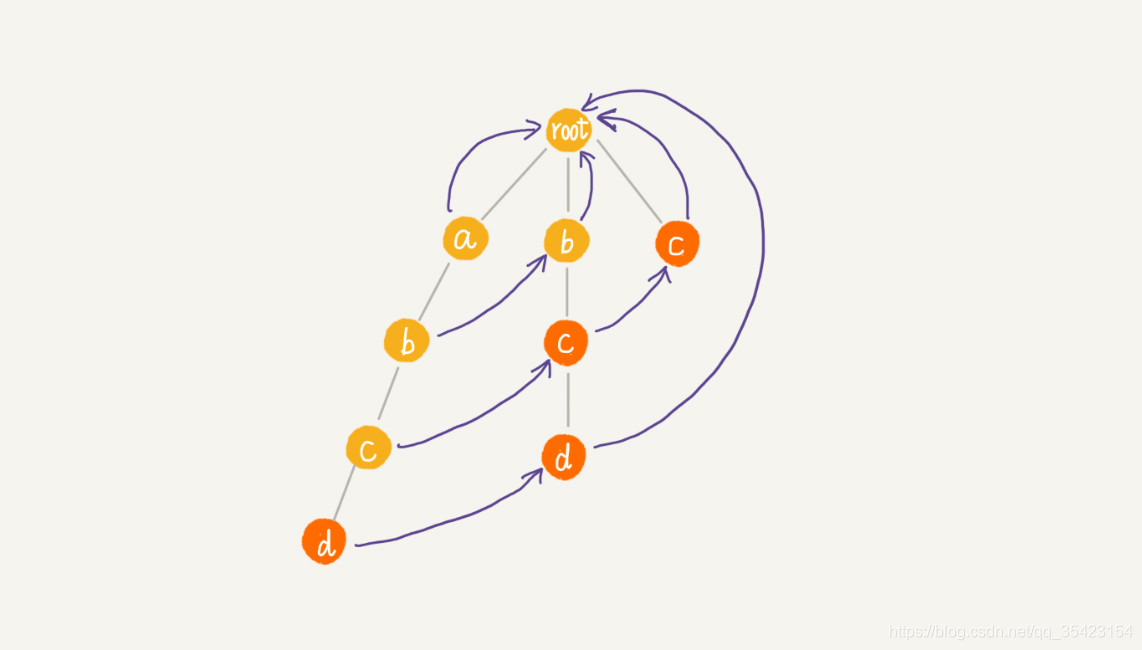
ac_am_6

简单描述上图的查询流程

  1. 第一轮查询a，进入最左边的模式串，此时不够成单词，失败指针指向root，查询不到
  2. 第二轮查询b，ab不构成单词，进入失败指针b，b也不构成单词
  3. 第三轮查询c，abc不构成单词，进入失败指针c，此时bc匹配成功。接着进入失败指针c，此时c也匹配成功。
  4. 第四轮查询，abcd构成单词，查询成功，接着进入失败指针d，bcd也成功匹配。

所以结果cd，abcd，bcd，c全部匹配成功

AC自动机的算法流程十分复杂，文字很难描述，所以我直接给出代码，并在其中写明了注释，如果还是搞不懂的可以一步一步进行调试。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
//匹配模式串
void AC::match(const string& str) const
{
    if (str.empty())
    {
        return;
    }
    ACNode* parent = _root;
    for (int i = 0; i < str.size(); i++)
    {
        ACNode* sub = parent->_subNode[str[i]];
        //如果子节点中找不到，则前往失败指针中寻找
        while (sub == nullptr && parent != _root)
        {
            parent = parent->_fail;
        }
        sub = parent->_subNode[str[i]];
        //如果还是找不到，则说明已经没有任何匹配的了，直接回到根节点
        if (sub == nullptr)
        {
            parent = _root;
        }
        else
        {
            parent = sub;   //继续查找下一个字符
        }
        ACNode* result = parent;
        while (result != _root)
        {
            //如果当前构成一个单词
            if (result->_isEnd == true)
            {
                //输出匹配的模式串
                cout << str.substr(i - result->_length + 1, result->_length) << endl;
            }
            result = result->_fail;     //如果无法构成一个单词，则继续前往失败指针中继续寻找
        }
    }
}

完整代码

除了匹配和失败指针的构建，其他步骤都和Trie树一样，所以可以直接复用之前的代码。
需要注意的是，每次插入和删除之后都必须重新构建失败指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
#include<unordered_map>
#include<string>
#include<vector>
#include<queue>
#include<iostream>
using namespace std;
namespace lee
{
    struct ACNode
    {
        ACNode(char data = ' ')
            : _data(data)
            , _isEnd(false)
            , _length(-1)
            , _fail(nullptr)
        {}
        char _data;		//当前字符
        bool _isEnd;	//标记当前是否能构成一个单词
        int _length;    //当前模式串长度
        ACNode* _fail;  //失败指针
        unordered_map<char, ACNode*> _subNode;	//子节点
    };
    class AC
    {
    public:
        AC()
            : _root(new ACNode())
        {}
        ~AC()
        {
            delete _root;
        }
        //防拷贝
        AC(const AC&) = delete;
        AC& operator=(const AC&) = delete;
        void buildFailurePointer();             //构建失败指针
        void match(const string& str) const;    //匹配模式串
        void insert(const string& str);         //插入字符串
    private:
        ACNode* _root;  //根节点
    };
    //插入字符串
    void AC::insert(const string& str)
    {
        if (str.empty())
        {
            return;
        }
        ACNode* cur = _root;
        for (size_t i = 0; i < str.size(); i++)
        {
            //如果找不到该字符，则在对应层中插入
            if (cur->_subNode.find(str[i]) == cur->_subNode.end())
            {
                cur->_subNode.insert(make_pair(str[i], new ACNode(str[i])));
            }
            cur = cur->_subNode[str[i]];
        }
        cur->_isEnd = true;         //标记该单词存在
        cur->_length = str.size();  //标记该单词长度
    }
    //构建失败指针
    void AC::buildFailurePointer()
    {
        //借助队列来完成层序遍历
        queue<ACNode*> q;
        q.push(_root);
        while (!q.empty())
        {
            ACNode* parent = q.front();
            q.pop();
            //遍历所有孩子节点
            for (auto& sub : parent->_subNode)
            {
                //如果父节点节点为根节点，则将孩子节点的失效指针全部设置为根节点
                if (parent == _root)
                {
                    sub.second->_fail = _root;
                }
                else
                {
                    ACNode* failParent = parent->_fail;    //父节点的失败指针
                    while (failParent != nullptr)
                    {
                        auto failChild = failParent->_subNode.find(sub.second->_data);    //寻找失败指针中是否存在一个子节点能与我们的子节点匹配
                        if (failChild != failParent->_subNode.end())   //如果存在，则这个子节点就是我们子节点的失败指针
                        {
                            sub.second->_fail = failChild->second;
                            break;
                        }
                        //如果找不到，则继续向上，寻找失败指针的失败指针是否有这么一个节点
                        failParent = failParent->_fail;
                    }
                    //如果一直找到最顶上也找不到，则将失败指针设置为根节点
                    if (failParent == nullptr)
                    {
                        sub.second->_fail = _root;
                    }
                }
                //将子节点加入队列中
                q.push(sub.second);
            }
        }
    }
    //匹配模式串
    void AC::match(const string& str) const
    {
        if (str.empty())
        {
            return;
        }
        ACNode* parent = _root;
        for (int i = 0; i < str.size(); i++)
        {
            ACNode* sub = parent->_subNode[str[i]];
            //如果子节点中找不到，则前往失败指针中寻找
            while (sub == nullptr && parent != _root)
            {
                parent = parent->_fail;
            }
            sub = parent->_subNode[str[i]];
            //如果还是找不到，则说明已经没有任何匹配的了，直接回到根节点
            if (sub == nullptr)
            {
                parent = _root;
            }
            else
            {
                parent = sub;   //继续查找下一个字符
            }
            ACNode* result = parent;
            while (result != _root)
            {
                //如果当前构成一个单词
                if (result->_isEnd == true)
                {
                    //输出匹配的模式串
                    cout << str.substr(i - result->_length + 1, result->_length) << endl;
                }
                result = result->_fail;     //如果无法构成一个单词，则继续前往失败指针中继续寻找
            }
        }
    }
};

这里我给出几个敏感词进行测试，查看是否能够全部匹配出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int main()
{
    lee::AC ac;
    ac.insert("ass");
    ac.insert("fuck");
    ac.insert("shit");
    ac.insert("cao");
    ac.insert("sb");
    ac.insert("nmsl");
    ac.insert("dead");
    ac.buildFailurePointer();
    ac.match("fuckyou,nmslsb");
    return 0;
}

匹配成功，这里的匹配功能其实就已经是敏感词过滤的一个原型代码了，我们只需要将匹配到的词替换成屏蔽符号*即可，为了方便演示所以我才改成输出模式串
ac_am_7

性能计算

AC自动机的构建包含两个步骤，Trie树的构建以及失败指针的构建。
Trie树构建的时间复杂度
假设模式串平均长度为M，个数为Z，则构建Trie树的时间复杂度为O(M * Z)

失败指针构建的时间复杂度
假设Trie树中总节点数为K，模式串平均长度为M
失败指针构建的时间复杂度为O(M * K)

匹配的时间复杂度
匹配需要遍历主串，所以这一部分的时间复杂度为O(N)，N为主串长度。
我们需要去匹配各个模式串，假设模式串平均长度为M，则匹配的时间复杂度为O(N * M)。

并且由于敏感词一般不会很长，所以在实际情况下，这个时间复杂度可以近似于O(N)

但是在下图这种大部分的失效指针都指向根节点时，AC自动机的性能会退化的跟Trie树一样、

ac_am_8